如果你對數學有一定的興趣，你可能聽說過黎曼球面，即一個把無窮遠的點映射到有限平面上的神奇結構。這個結構不僅在復分析和代數幾何中有重要的應用，而且還揭示了無窮的本質和可能性。
讓我們從一個簡單的問題開始：如何在二維平面上表示無窮遠？也就是說，如何用有限的坐標來表示一個距離原點無限遠的點？
一個直觀的想法是，我們可以用極坐標來表示平面上的點，即用距離原點的長度和與正半軸夾角來確定一個點。例如，（1， π/4） 表示距離原點為 1 的點，其與正半軸夾角為 π/4。那麼，我們可以用 （r， θ） 來表示任意一個平面上的點，其中 r 是長度，θ 是角度。如果 r 趨于無窮大，那麼這個點就趨于無窮遠。
但是這樣有一個問題：當 r 趨于無窮大時，θ 的值并不唯一。也就是說，不同方向上趨于無窮遠的點都可以用 （r， θ） 來表示，只要 r 足夠大。這樣就失去了區分不同方向上無窮遠點的能力。
為了解決這個問題，我們需要引入一個新的概念：立體投影。
立體投影是一種將三維空間中的對象映射到二維平面上的方法。具體來說，我們可以想象在三維空間中有一個單位球（半徑為 1 的球），它與 xy 平面相切于原點。然后我們從球心出發畫一條射線，并看它與球和平面相交于哪些點。
如果射線與球相交于 A 點（除了原點外），那麼它也必然與平面相交于 B 點（除了原點外）。反之亦然。因此，我們可以建立 A 點和 B 點之間的一一對應關系，并把 A 點映射到 B 點。
注意，在這種映射下，并不是所有三維空間中的點都能被映射到二維平面上。只有位于單位球外部或者位于單位球內部但不在 xy 平面上方或者下方（即 z 軸）的點才能被映射到二維平面上。如果射線與球相交于原點，那麼它就不與平面相交于任何點。這意味著原點是一個特殊的點，它不能被映射到二維平面上。
那麼，我們能不能把原點也映射到二維平面上呢？答案是可以，但我們需要做一些改動。我們可以把原點看作是一個無窮遠的點，即距離球心無限遠的點。這樣，當我們從球心出發畫一條射線時，如果它與球相交于原點，那麼它就相當于沿著 z 軸方向延伸到無窮遠處。而當我們把這個無窮遠的點映射到二維平面上時，我們可以用一個特殊的符號來表示它：∞。
這樣，我們就實現了從三維空間中的單位球（包括原點）到二維平面（加上∞）的一一對應關系。這個對應關系就叫做立體投影。
現在，讓我們回到最初的問題：如何在二維平面上表示無窮遠點？有了立體投影的概念后，答案就很明顯了：我們只需要把二維平面看作是三維空間中的單位球（包括原點）經過立體投影得到的結果。
換句話說，我們可以把每一個平面上的點都對應到一個單位球上的點，而且這個對應是一一的，即不同的平面上的點對應到不同的球面上的點，反之亦然。這樣，我們就可以用球面上的點來表示平面上的點，而且還可以用球面上的原點來表示平面上的無窮遠點。
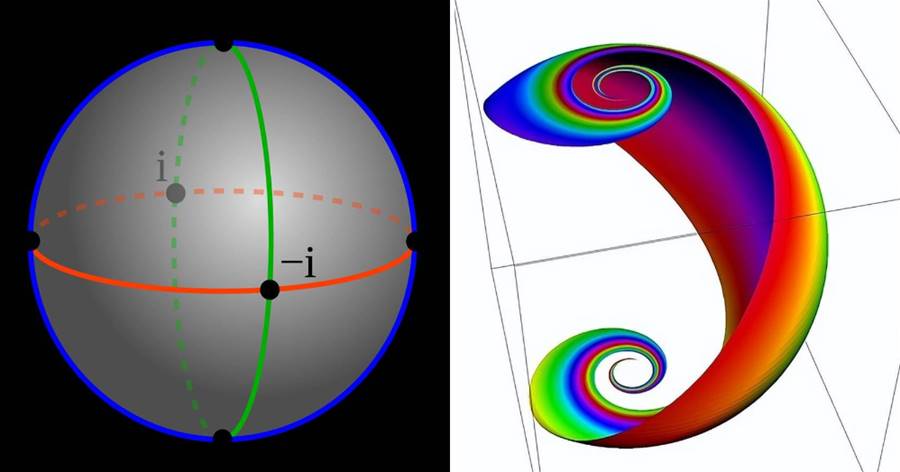
這個單位球（包括原點）就叫做黎曼球面，它是一個復分析中常用的工具。復分析是研究復數函數（即以復數為自變量和因變量的函數）的性質和規律的數學分支。復數是一種擴展了實數范圍的數，它由實部和虛部組成，例如 a + bi 就是一個復數，其中 a 和 b 都是實數，i 是虛數單位，滿足 i^2 = -1。
我們可以把每一個復數都看作是一個二維平面上的點，其中橫坐標為實部，縱坐標為虛部。
這樣，我們就可以用黎曼球面來表示復數，而且還可以用黎曼球面上的原點來表示無窮遠點。這樣做有什麼好處呢？一個好處是，我們可以用黎曼球面上的距離來衡量復數之間的相似性。例如，如果兩個復數在平面上很接近，那麼它們在黎曼球面上也很接近；如果兩個復數在平面上相差很大，那麼它們在黎曼球面上也相差很大；如果一個復數趨向于無窮遠，那麼它在黎曼球面上趨向于原點。
另一個好處是，我們可以用黎曼球面來研究一些特殊的復數函數，例如 f（z） = 1/z。這個函數的意思是，對于任何一個非零的復數 z，我們可以用 1/z 來表示它的倒數。
這個函數有一個特殊的性質，就是它把黎曼球面上的每一個點都映射到另一個點，而且這個映射是一一的，即不同的球面上的點被映射到不同的球面上的點，反之亦然。這樣，我們就可以用 f（z） 來表示黎曼球面上的變換。
這個變換有什麼特點呢？一個特點是，它把原點（無窮遠點）映射到自身；另一個特點是，它把球面上的每一個點都映射到它的對稱點，即與原點相距相等但方向相反的點。例如，如果 z = 1 + 2i，那麼 f（z） = 1/（1 + 2i） = （1 - 2i）/5，這兩個點在球面上是對稱的。
這個變換還有一個特點，就是它保持了球面上的角度不變。
黎曼球面還有一個重要的性質，就是它可以用來表示球面上的幾何。我們知道，球面上的距離和角度與平面上的不同，例如，球面上的最短路徑是大圓弧，而不是直線；球面上的三角形的內角和大于 180 度，而不等于 180 度。那麼如何用復數來描述球面上的幾何呢？
一個方法是用立體投影（conformal mapping）。立體投影是一種把球面上的點映射到平面上的點的方法，具體做法是從球面上任意一點引一條直線穿過原點（無窮遠點），與平面相交于另一點，這樣就得到了一個映射。
立體投影有一個優點，就是它也是一種共形映射，即它也保持了球面上的角度不變。這樣，我們就可以用平面上的復數來表示球面上的幾何，并且不失去角度的信息。例如，如果我們想要知道球面上兩條曲線的交角，我們只需要把它們投影到平面上，然后用復數來計算它們的交角。
立體投影還有一個缺點，就是它不能完整地表示球面上的所有點。因為無窮遠點是沒有對應的平面上的點的，所以我們需要把無窮遠點單獨考慮。這樣，我們就得到了一個擴展的復平面（extended complex plane），即在復平面上加一個無窮遠點 ∞。
黎曼球面的一個重要應用是在復分析中。復分析是研究復變函數（complex function）的數學分支，復變函數是指把復數映射到復數的函數，例如 f（z） = z^2 + 1。復分析中有一個基本的定理叫做里奧維爾定理（Liouville’s theorem），它說：
如果一個復變函數在整個擴展的復平面上都是解析（analytic）的，并且有界（bounded），那麼它必然是一個常數。
解析（analytic）這個概念很重要，它意味著這個函數在任何一點都可以用泰勒級數（Taylor series）來展開，并且這個級數收斂到這個函數。有界（bounded）就是說這個函數的值不會無限大或無限小。
那麼，為什麼要在擴展的復平面上考慮解析性呢？因為有些函數在復平面上是解析的，但是在無窮遠點不是。例如，f（z） = 1/z 就是這樣一個函數，它在復平面上除了 z = 0 這一點外都是解析的，但是當 z 趨向于無窮大時，它的值趨向于零。如果我們把無窮遠點加進來，那麼這個函數就不再是解析的了，因為它在無窮遠點不連續。
但是如果我們用黎曼球面來表示這個函數，情況就不一樣了。因為立體投影把無窮遠點映射到了球面的北極 （0， 0， 1），而把原點映射到了球面的南極 （0， 0， -1），所以 f（z） = 1/z 在黎曼球面上就變成了一個交換北極和南極的映射。這個映射其實就是沿著經線旋轉球面 180 度。這樣一來，f（z） = 1/z 在黎曼球面上就變成了一個連續且可微（differentiable）的函數，也就是說，在黎曼球面上它是解析的。
個例子說明了黎曼球面的一個重要性質，就是它是一個緊致（compact）的拓撲空間，即它是一個有界且閉合的空間。這樣，任何在黎曼球面上連續的函數都必然是有界的，因為它不能超出球面的范圍。這就使得里奧維爾定理在黎曼球面上更加簡潔，只需要說：
如果一個復變函數在整個黎曼球面上都是解析的，那麼它必然是一個常數。
這就是說，在黎曼球面上，解析性和有界性是等價的。
黎曼球面還有一個重要的性質，就是它是一個黎曼面（Riemann surface），即它是一個復流形（complex manifold）。
黎曼面的重要性在于，任何兩個黎曼面之間都存在一個雙全純映射（biholomorphic map），也就是說，一個保持解析性和方向的一對一映射。這意味著任何兩個黎曼面都可以互相變換而不改變它們的本質屬性。這就給了我們一種分類黎曼面的方法，就是看它們有多少個互不等價的雙全純映射。例如，復平面和黎曼球面之間只有一個雙全純映射，就是立體投影。所以我們說復平面和黎曼球面屬于同一類黎曼面。
黎曼面的分類問題是一個非常深刻而困難的問題，它涉及到了復分析、代數幾何、拓撲學等多個數學分支。直到 20 世紀初，這個問題才得到了完整的解決。其中一個關鍵的結果是黎曼-羅赫定理（Riemann-Roch theorem），它給出了一個黎曼面上雙全純映射的數量和它的虧格（genus）之間的關系。虧格是一種用來度量黎曼面復雜性的數，它等于黎曼面上洞的數量。例如，復平面和黎曼球面都沒有洞，所以它們的虧格都是零。而一個圓環或者一個甜甜圈則有一個洞，所以它們的虧格都是一。
黎曼-羅赫定理告訴我們，如果一個黎曼面有 g 個洞，那麼它和自身之間存在 g（g+1）/2 個不同的雙全純映射。這就意味著，如果我們知道了一個黎曼面有多少個洞，我們就可以知道它有多少種不同的方式來變換自身而不改變本質屬性。
黎曼面的分類問題還有一個更深刻的結果，就是黎曼映射定理（Riemann mapping theorem），它說：
如果一個黎曼面是單連通的，那麼它和單位圓盤之間存在一個唯一的雙全純映射。
這就是說，任何一個沒有洞的黎曼面都可以變換成一個單位圓盤，而且只有一種變換方法。這個定理給出了一種極其強大的工具，就是把復雜的黎曼面簡化成一個簡單的圓盤。例如，我們可以用這個定理來證明基本定理（fundamental theorem）：
如果一個復變函數在整個復平面上都是解析的，并且不是常數，那麼它必然存在至少一個零點。
這個定理可以用黎曼球面和單位圓盤之間的雙全純映射來證明。我們只需要把復平面上沒有零點的解析函數映射到黎曼球面上，然后再把黎曼球面上沒有零點的解析函數映射到單位圓盤上。這樣我們就得到了一個在整個單位圓盤上沒有零點的解析函數。但是根據最大模原理（maximum modulus principle），這樣的函數必然是常數。所以原來在復平面上沒有零點的解析函數也必然是常數。
總之，黎曼球面是一個非常美麗而神奇的數學對象，它不僅可以讓我們用有限的方式來理解無窮，還可以讓我們用簡單的方式來理解復雜。它是復分析、代數幾何、拓撲學等多個數學領域的重要工具，也是物理學中描述時空結構和量子力學中描述粒子態的基本概念。它還與著名的黎曼猜想（Riemann hypothesis）有著密切的聯系，這是一個至今未解決的數學難題，它涉及到了素數分布和黎曼ζ函數（Riemann zeta function）在黎曼球面上的零點。
